Introducción
El sistema decimal es universalmente empleado para representar cantidades en el mundo real. Los sistemas electrónicos digitales tienen que recoger la información y convertirla en dígitos binarios para procesarla internamente. Así mismo, cuando la información es procesada, es necesario convertir esta información, por lo general a decimal antes de llevarla al mundo exterior. En realidad, no se manejan solamente estos dos sistemas, en la práctica se hace necesario utilizar códigos que facilitan el manejo de otras características.
SANDRA LILIANA CARMONA
CESAR AUGUSTO PARRA
JOHAN SEBASTIAN OSORIO
SANDRA LILIANA CARMONA
CESAR AUGUSTO PARRA
JOHAN SEBASTIAN OSORIO
Codificador
Los bloques funcionales combinacionales son circuitos implementados con puertas lógicas, que se comercializan en circuitos integrados de escala de integración media (MSI, Medium Scale Integration) y que realizan operaciones útiles como comparaciones, selección de datos, conversiones de un código a otro, etc.
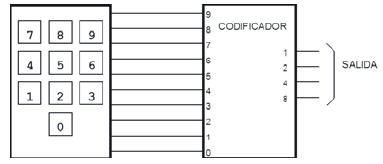
Los circuitos codificadores son el primer bloque de muchos sistemas digitales, ya que realizan la conversión de los números decimales a un código binario. Son el enlace entre los teclados y los sistemas digitales en la forma que se representa en la figura.
Al pulsar uno de los números, se activa a línea correspondiente en la salida del teclado.Supóngase que la tecla pulsada es el 2. En la salida del teclado se tendría:
La combinación de ceros y unos en la salida del teclado no es un número binario. Si fuese así, y el bit de mayor peso fuese el correspondiente a la entrada 9 del codificador, el número sería el 0000000100, es decir, el 4. El 1 en la salida 2 del teclado informa de que la tecla pulsada es la correspondiente al 2 decimal y por eso esa combinación de unos y ceros puede ser considerada un número decimal. El codificador recibe en su entrada números decimales y los convierte (codifica) a binario BCD (8421).
Las señales de entrada a un circuito codificador pueden no provenir de un teclado. En la figura aparecen 10 posibles fuentes de señal para las entradas del codificador que pueden provenir de sensores (temperatura, presión, humedad, luz, etc) o ser la salida de un sistema digital como un teclado de un ordenador, una impresora, una memoria o cualquier otro circuito. Cada sensor o circuito se distingue de los demás por el número decimal que se le asigna. A este número se le llama dirección.
El codificador convierte la dirección decimal del sensor o circuito que se activa en una dirección codificada en BCD.
Decodificador
Un decodificador o descodificador es un circuito combinacional, cuya función es inversa a la del codificador, esto es, convierte un código binario de entrada (natural, BCD, etc.) de N bits de entrada y M líneas de salida (N puede ser cualquier entero y M es un entero menor o igual a 2N), tales que cada línea de salida será activada para una sola de las combinaciones posibles de entrada
La función básica del decodificador es detectar la presencia de una determinada combinación de bits en las entradas e indicar la presencia de este código mediante la activación de una línea.
Decodificador 2-4
Un decodificador 2-4 indica que tiene dos entradas y cuatro salidas debido a que 2 = 4. Este decodificador tiene la siguiente tabla de verdad.La implementación de este decodificador es la siguiente:
Este decodificador se puede conseguir en el mercado como el CI 74LS139.
Este circuito tiene dos decodificadores internamente y sus salidas son activas a nivel bajo. Además tiene una entrada denominada G activa a nivel bajo, que permite habilitar o inhabilitar el circuito. La representación de este circuito se presenta en la siguiente figura
Decodificador 3-8
Un decodificador 3-8 indica que tiene tres entradas y ocho salidas debido a que 2 = 8. Este decodificador tiene la siguiente tabla de verdad.
La implementación de este decodificador es la siguiente:
Este decodificador se puede conseguir en el mercado como el CI 74LS138.
Este circuito tiene un decodificador y sus salidas son activas a nivel bajo. Además tiene tres entradas denominadas G1, G2A y G2B que permiten habilitar o inhabilitar el circuito. G1 es activa a nivel alto y G2A y G2B son activas a nivel bajo. La representación de este circuito se presenta en la siguiente figura.
Multiplexor
Los multiplexores son circuitos que seleccionan la información digital, procedente de distintas fuentes, para transmitirla por una única línea.
Entradas de selección y entradas de datos La figura representa un circuito multiplexor. Las entradas S1 y S0 se llaman entradas de selección y las entradas D0 a D3 entradas de datos.
En las entradas de selección se utiliza un código binario de 2 bits para seleccionar una de las 4 entradas de datos. La información (0 o 1) presente en la entrada de datos seleccionada, aparecerá en la salida de datos. La tabla de verdad siguiente resume el funcionamiento del multiplexor.
La tabla de verdad anterior muestra el multiplexor 4-1, locual indica que tiene cuatro entradas de un bit, por consiguiente tiene dos líneas de selección y una sola salida de un bit.
La implementación de este circuito es el siguiente:
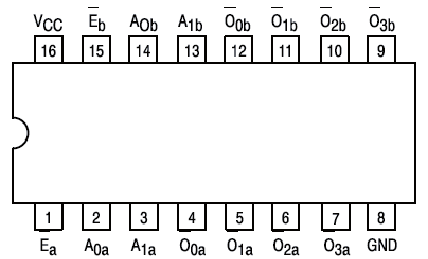
El CI 74LS153 contiene dos multiplexores 4-1. La siguiente figura 4.21 representa este circuito. En este circuito las líneas activas a nivel bajo Ea y Eb son habilitadoras, es decir, que el circuito funcionara si en estas entradas hay un 0 lógico.
Multiplexor cuádruple 2-1
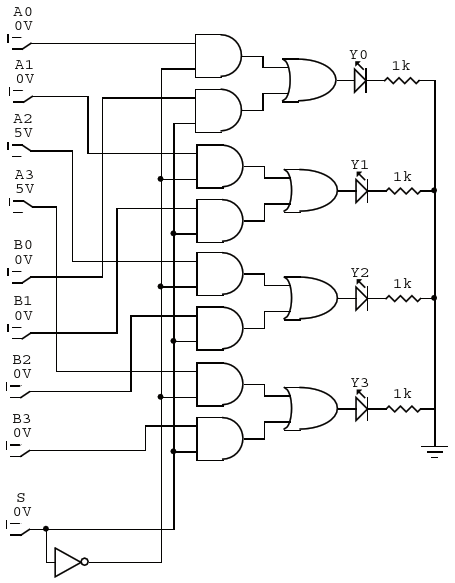
Este multiplexor indica que tiene dos entradas de cuatro bits, por consiguiente tiene una sola línea de selección y una sola salida de cuatro bits. Dada la definición, la tabla de verdad para este multiplexor sería la siguiente.
La tabla anterior indica que si la línea de selección es 0, entonces la salida contendrá lo que tiene la entrada A de 4 bits. Si la línea de selección es 1, entonces la salida contendrá lo que tiene la entrada B de 4 bits.
La implementación de este circuito es la siguiente:
El CI 74LS157 contiene un multiplexor 2-1 de 4 bits. La siguiente figura 4.23 representa este circuito. En este circuito la línea activa a nivel bajo E es un habilitador, es decir, que el circuito funcionará si en esta entrada hay un 0 lógico.
Conversor de Código
El conversor de código es un circuito similar a un decodificador o un codificador, pero utiliza otros códigos a la entrada o a la salida; la diferencia es que tendremos tantos conversores de código como códigos que queramos convertir y, por tanto, para diseñar un conversor de código es necesario primeramente definir los códigos de entrada y de salida que manejará el circuito.
Los códigos más utilizados son el binario BCD 8421, octal, hexadecimal y el decimal, los dispositivos digitales pueden procesar solamente los bits "1" y "0" . Estas largas cadenas de 1 y 0 son difíciles de comprender por las personas. Por esta razón se necesitan los conversores de códigos para traducir el lenguaje de la gente al lenguaje de la máquina.
Un ejemplo de conversor de código es una sencilla calculadora manual, la cual está constituida por un dispositivo de entrada llamado teclado. Entre el teclado y la unidad central de tratamiento "CPU" hay un codificador, que traduce el número decimal pulsado en el teclado a código binario. La "CPU" realiza su operación en binario y produce un resultado en código binario. El decodificador traduce el código binario de la CPU a un código especial que hacen que luzcan los segmentos adecuados en el visualizador de siete segmentos.
Conversión de Binario a Decimal
Cualquier número Binario puede ser convertido en su equivalente ENTERO Decimal. La forma de hacerlo es sumar en el número Binario todas las posiciones que contengan el valor 1. Veamos el ejemplo de conversión del número Binario de 4 bits (1010), Esto se podría expresar de la siguiente manera:
• Número Binario de 4 Bits: 1010
• Conversión por posiciones: (1 x 2 a la 3ª ) + (0) + (1 x 2 a la 1ª ) + (0)
• Número Decimal: 8 + 0 + 2 + 0 = 10
Convirtiendo un número con 6 Bits:
• Número Binario de 8 Bits: 100110
• Conversión por posiciones: (1x2 a la 5ª)+(0)+(0)+(1x2 a la 2ª)+(1x2 a la 1ª)+(0)
• Número Decimal: 32 + 0 + 0 + 4 + 2 = 38
Conversión de Decimal a Binario
La conversión de un número decimal ENTERO a su equivalente Binario, puede lograrse de dos formas diferentes.
La Primera Forma es utilizar de forma inversa el método anterior, comenzamos por restar los valores de los bits (potencias de 2) más cercanos al valor decimal hasta llegar a cero, luego se completa con ceros los valores faltantes entre los bits, convertir 150:
- La potencia de 2 más cercana a 152 es 128 (2 a la 7ª , Octavo Bit) 152 -128=22
- La potencia de 2 más cercana a 22 es 16 (2 a la 4ª , Quinto Bit) 22 - 16 =6
- La potencia de 2 más cercana a 6 es 4 (2 ala 2ª , Tercer Bit) 6-4=2
- La potencia de 2 más cercana a 2 es 2 (2 ala 1ª , Segundo Bit) 2-2 = 0
La segunda es la llamada "División Repetida", esta manera de conversión se basa en repetir la división del número decimal entre dos, hasta llegar al cero. Si el residuo de la división no es un número entero, se marca un 1 y se toma el número entero para volver a dividir entre dos, cuando el Residuo es un número entero, se marca un cero y se toma el número para volver a dividir entre dos. El residuo de la primero división es el (LSB, primer Bit), el residuo de la última división es el (MSB, último Bit). Esto se ilustra así:
Conversión del Sistema Octal a Decimal
La conversión de un número octal a uno decimal es muy sencilla, sólo necesitamos multiplicar cada uno de los dígitos por el valor que corresponde a su posición. Para convertir el número 435 comenzamos por:
- Tres posiciones 8 a la 2ª , 8 la 1ª , 8 a la 0.
- Primer Bit Octal (5 x 8 a la 0) = 5 x 1 = 5
- Segundo Bit Octal (3 x 8 a la 1ª ) = 3 x 8 = 24
- Tercer Bit Octal (4 x 8 a la 2ª ) = 4 x 64 = 256
- Número decimal = (5 + 64 + 256ª ) = 285
Conversión del Sistema Decimal a Octal
Un número Decimal ENTERO puede convertirse al sistema Octal utilizando también la "División Repetida", pero en este caso, nuestro factor para dividir será el 8, de la misma manera, el residuo de la primera división será el LSB, y el residuo de la última división será el MLB. Para poder saber el número que se convierte en cada Bit octal, se multiplica la fracción del residuo por 8, y se toma el número entero para volver a dividir entre 8. Convertir el decimal 150 a Octal nos daría:
Conversión del Sistema Octal a Binario
Una de las grandes ventajas del Sistema Octal, es que fácilmente podemos convertir un número Octal al Sistema Binario. Este proceso se realiza convirtiendo cada número Octal en su equivalente del Sistema Binario, pero con la diferencia que se utilizan forzosamente 3 Bits. De manera que Cada Bits Octal es convertido por separado en su equivalente Binario. Convertir el número Octal 561 al sistema Binario sería:
Conversión del Sistema Binario a Octal
El proceso de conversión de números Binarios ENTEROS al Sistema Octal se logra invirtiendo el proceso descrito arriba. Lo primero que hacemos es agrupar todos los bits del número Binario en grupos de tres, iniciando con el LSB (Primer Bit). Ya que tenemos separados los Bits, se convierte cada trío a su equivalente del Sistema Octal. En el caso de que en el último grupo de Bits (MLB) no se pueda hacer un trío, se agregan ceros hasta lograrlo.
Convertir un número Binario que tiene sus tríos completos, 101110001 al Sistema Octal sería:
- Se agrupan los bits en tríos (101110001) = 101 - 110 - 001
- Se convierte el Primer trío (donde se encuentra el LSB) 001 = 1
- Se convierte el Segundo trío 110 = 6
- Se convierte el Tercer trío (donde se encuentra el MSB) 101 = 5
- Número Octal = 561
Convertir un número Binario que no tiene sus tríos completos, 10101110001 al Sistema Octal sería:
- Se agrupan los bits en tríos (10101110001) = 10 - 101 - 110 - 001
- Completar los tríos (agregando un 0) = 010 - 101 - 110 - 001
- Se convierte el Primer trío (donde se encuentra el LSB) 001 = 1
- Se convierte el Segundo trío 110 = 6
- Se convierte el Tercer trío 101 = 5
- Se convierte el Cuarto trío (donde se encuentra el MSB) 010 = 2
- Número Octal = 2561
Conversión del Sistema Hexadecimal a Decimal
Para convertir un número del Sistema Hex a su equivalente Decimal necesitamos primero recordar que la posición de los números en del Sistema Hex, basan su valor en una potencia de 16. El Primer Bit (LSB) sería 16 a la 0 = (1), el segundo Bit sería 16 a la 1ª = (16), el tercer Bit sería 16 a la 2ª = (256), aumentando las potencias de 16 hasta llegar al último Bit (MLB). La conversión se realiza entonces de la siguiente manera:
- Convertir el número Hex 182 al Sistema Decimal
- Convertir el número Hex 6AF al Sistema Decimal
Conversión del Sistema Decimal a Hexadecimal
Nuevamente acudimos a la "División repetida para lograr esta conversión, al igual que en los ejemplos anteriores (división por 2 para convertir Decimal a Binario, y división por 8 para convertir Decimal a Octal), pero esta vez, la división será por 16. Al igual que antes, si el residuo contiene fracciones decimales, se multiplican por 16 y se toma el número entero para la nueva división por 16. Convertir los números 1711 y 386 del Sistema Decimal s Hex.
Conversión del Sistema Hexadecimal a Binario
Al igual que en la conversión del Sistema Octal (que se convierten en tríos de Bits Binarios), en la conversión del Sistema Hexadecimal a Binario, cada Bit Hex se convierte en cuartetos de Bits Binarios.
Convertir el número del Sistema Hex 8A1 a Binario sería:
Conversión del Sistema Binario a Hexadecimal
La forma de convertir un número del Sistema Binario a Hex, es completamente opuesta a la presentada arriba. Se forman cuartetos de Bits Binarios (comenzando desde el LSB) hasta el MSB. Al igual que en la conversión de Sistema binario a Octal, en caso de que no se completen los cuartetos, se agregan los ceros necesarios para completar lo últimos cuatro Bits.
Convertir el número del Sistema Binario 100010100001 a Hex sería:
- Se agrupan los bits en cuartetos (100010100001) = 1000 - 1010 - 0001
- Se convierte el Primer cuarteto (donde se encuentra el LSB) 0001= 1
- Se convierte el Segundo trío 1010 = 10 = A
- Se convierte el Tercer trío (donde se encuentra el MSB) 1000 = 8
- Número Hex = 8A1
Sumador
En los sistemas digitales pueden presentarse situaciones en las que sea necesario hacer la suma de dos números que, lógicamente, estarán expresados en binario. Seguidamente se describen los circuitos lógicos que realizan sumas binarias.
Los sumadores son circuitos muy importantes para diferentes tipos de sistemas digitales en los que se procesan datos numéricos. Para construir un sumador básico es necesario conocer las reglas de la suma binaria. Simplemente se tienen cuatro posibilidades:
0+0=0
0+1=1
1+0=1
1+1=10
Entonces con base en las ecuaciones anteriores se hace la siguiente implementación en la figura
Sumador completo o Full-A A dder (F-A A )
Aritmética en los códigos binarios 5 Un sumador completo es un circuito que suma dos bits, como el semisumador, pero además tiene en cuenta un posible acarreo de una suma anterior y lo incorpora a la suma que realiza. Las entradas del circuito serán tres, una para cada bit a sumar más el acarreo; sean a, b y cj respectivamente. Las salidas del circuito, funciones de las entradas, serán dos, ya que la suma puede tener hasta dos bits como resultado; sean s y c0 como en el H-A. Según las reglas aritméticas, la relación entre los bits de entrada y los de salida viene dada por la tabla de verdad siguiente:
El esquema del circuito sumador completo será, por lo tanto:
También se puede comprobar (con la ayuda de una tabla de verdad, por ejemplo) que un sumador completo se puede obtener a partir de dos semisumadores del modo siguiente:Sumador paralelo con acarreo serie
Un sumador paralelo es un circuito que suma dos números de más de un bit cada uno, a partir de la disposición simultánea de todos los bits de los operandos. Más adelante se verán los sumadores serie, en los que se va disponiendo de los bits de los operandos de modo secuencial, unos después de otros, desde los de menos peso hasta los de más peso.
Un sumador paralelo se puede construir a partir de tantos circuitos sumadores completos como bits tengan los operandos. Cada sumador completo hace la suma parcial de un bit de cada operando (entradas a y b) más el bit de acarreo (entrada ci ) de la suma parcial anterior, y proporciona un bit de resultado para la suma (salida so ) más un acarreo de salida para la suma de los bits siguientes (salida s0). Además, se tendrá en cuenta que:
- En el primer par de bits a sumar (los LSB) no existirá acarreo anterior, por lo que en esa etapa se puede emplear un semisumador o un sumador completo con entrada ci =0.
- En el último par de bits a sumar (los MSB) el acarreo no se suma a ninguna etapa siguiente, por lo que este acarreo será el último bit de la suma.
Un sumador en paralelo de 4 bits se implementa mediante 4 sumadores completos. Los bits menos significativos, se implementan a la derecha. Los bits de orden más alto, se introducen en el sumador completo que está más a la derecha, aplicando los bits más significativos de cada número al sumador que está más a la izquierda (ver figura). La salida de acarreo de cada sumador se conecta a la entrada de acarreo del siguiente sumador de orden superior. Estos se denominan acarreos internos.El circuito integrado 74LS283, contiene un sumador en paralelo de 4 bits. La siguiente figura 4.4 muestra la distribución de pines de este circuito.
Restador
Implícitamente, a la operación de la resta va ligada la necesidad de representación de números positivos y negativos. En el caso del binario, el sistema de representación más sencillo, a priori, es el módulo-signo.
En la diferencia, cada bit del sustraendo se resta de su correspondiente bit del minuendo para formar el bit de la diferencia. El préstamo ocurre cuando el bit del minuendo es menor al bit del sustraendo, de tal forma que se presta un 1 de la siguiente posición significativa.
La resta se implementa mediante un sumador. El método consiste en llevar al minuendo a una de las entradas y el sustraendo en complemento 2 a la otra entrada.
Un medio restador es un circuito combinacional que sustrae dos bits y produce su diferencia. También tiene la salida para especificar si se ha tomado un 1. Se designa el bit minuendo por x y el bit sustraendo mediante y. Para llevar a cabo x – y, tienen que verificarse las magnitudes relativas de x y y. Si x >= y, se tienen tres posibilidades; 0 - 0 = 0, 1 – 0 = 1 y, 1 - 1 = 0. El resultado se denomina bit de diferencia. Si x < y, tenemos 0 – 1 y es necesario tomar un 1 de la siguiente etapa más alta. El 1 que se toma de la siguiente etapa más alta añade dos al bit minuendo, de la misma forma que en el sistema decimal lo que se toma añade 10 a un dígito minuendo. Con el minuendo igual a 2, la diferencia llega a ser 2 – 1 = 1. El medio restador requiere dos salidas. Una salida genera la diferencia y se denotará por el símbolo D. La segunda salida, denotada B para lo que se toma, genera la señal binaria que informa a la siguiente etapa que se ha tomado un 1. La tabla de verdad para las relaciones de entrada-salida de un medio restador ahora puede derivarse como sigue:
x y | B D
0 0 | 0 0
0 1 | 1 1
1 0 | 0 1
1 1 | 0 0
La salida que toma B es un 0 en tanto que x >= y. Es un 1 para x = 0 y y = 1. La salida D es el resultado de la operación aritmética 2B + x - y.
Las funciones booleanas para las dos salidas del medio restador se derivan de manera directa de la tabla de verdad:
D = x’y + xy’
B = x’y
Es interesante observar que la lógica para D es exactamente la misma que la lógica para la salida S en el medio sumador.
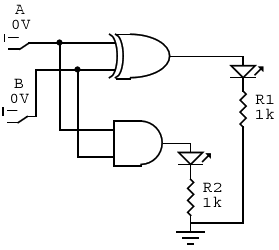
El logigrama del restador es el siguiente:
Su circuito topológico es el siguiente:
RESTADOR COMPLETO
Un restador completo es un circuito combinacional que lleva a cabo una sustracción entre dos bits, tomando en cuenta en un 1 se ha tomado por una etapa significativa más baja. Este circuito tiene tres entrada y dos salidas. Las tres entradas x, y y z, denotan al minuendo, sustraendo y a la toma previa, respectivamente. Las dos salidas, D y B, representan la diferencia y la salida tomada, respectivamente. La tabla de verdad para el circuito es como sigue:
x y z | B D
0 0 0 | 0 0
0 0 1 | 1 1
0 1 0 | 1 1
0 1 1 | 1 0
1 0 0 | 0 1
1 0 1 | 0 0
1 1 0 | 0 0
1 1 1 | 1 1
Los ocho renglones bajo las variables de entrada designan todas las combinaciones posibles de 1 y 0 que pueden tomar las variables binarias. Los 1 y 0 para las variables de salida están determinados por la sustracción de x – y – z. Las combinaciones que tienen salida de toma z = 0 se reducen a las mismas cuatro condiciones del medio sumador. Para x = 0, y = 0 y z = 1, tiene que tomarse un 1 de la siguiente etapa, lo cual hace B = 1 y añade 2 a x. Ya que 2 – 0 – 1, D = 1. Para x = 0 y yz = 11, necesita tomarse otra vez, haciendo B = 1 y x = 2. Ya que 2 – 1 – 1 = 0, D = 0. Para x = 1 y yz = 01, se tiene x – y – z = 0, lo cual hace B = 0 y D = 0. Por último, para x = 1, y = 1, z = 1, tiene que tomarse 1, haciendo B = 1 y x = 3 y, 3 –1 – 1 = 1, haciendo D = 1.
El circuito lógico implementado con compuertas es el siguiente:
El circuito topológico del restador completo es el siguiente:
Suscribirse a:
Entradas (Atom)